Bjorn's Hexakuro
Have fun with math puzzles
- a game -
What do you get when you cross Sudoku with Kakuro?
Hexakuro!

Game instructions (tap here for PDF)
Hexakuro™ is a hexagonal implementation of the number puzzle Kakuro (or Cross Sums). The object of the puzzle is to fill in each blank hexagon with a digit from 1 to 9 so that no digit is repeated in a continuous line of vertical or diagonal white hexagons. In addition, the digits in the line of hexagons must add up to the clue which is shown in a triangle at one end of the line. Unlike in Kakuro, where there is a clue for each row and column (on a rectangular grid), in Hexakuro many clues may be missing. In some cases, a hexagon may have no associated clue at all and the solution relies on your Sudoku skills based on having no number repeat in the contiguous vertical and diagonal hexagons. A well designed puzzle should have only a single solution.
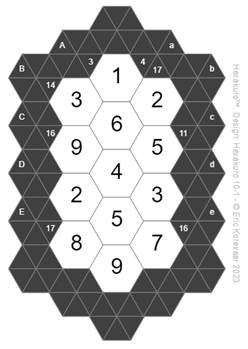
In this introduction we will solve a very small puzzle to see how things work. (This is puzzle Hexakuro 10-1 in the Online Game Ap if you want to try it yourself). The solution to a slightly more involved example puzzle can be found here.
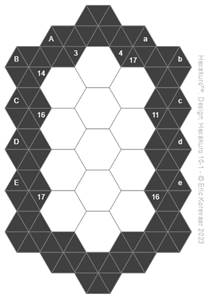 In
this example a coordinate system is marked on the outside of the puzzle to help
identify the hexagons. There are diagonals A,B,C,D,E slanting downwards from
left to right. There are diagonals a,b,c,d,e slanting downwards from right to
left. A hexagon at the intersection of two diagonals is labelled with both
coordinates. For instance the top hexagon in the middle is hexagon Aa.
In
this example a coordinate system is marked on the outside of the puzzle to help
identify the hexagons. There are diagonals A,B,C,D,E slanting downwards from
left to right. There are diagonals a,b,c,d,e slanting downwards from right to
left. A hexagon at the intersection of two diagonals is labelled with both
coordinates. For instance the top hexagon in the middle is hexagon Aa.
To start solving a puzzle, it is useful to look for hexagons that have two clues, with only one number being consistent with both of the clues.
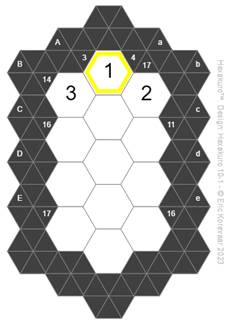
For example, Hexagon Aa is in diagonal “A” which has a sum of 3 for two hexagons. The only two digits that add up to 3 are in the set {1,2}. (That is, 1+2=3 and 2+1=3). Hexagon Aa is also in diagonal “a” which has a sum of 4 for two hexagons. The only sets of digits adding up to 4 are either {1,3} or {2,2}. But 2+2 is not allowed because the digits would have to repeat in the same diagonal. Since the only overlap between the set {1,2} and the set {1,3} is the number 1, we can deduce that 1 is the solution for hexagon Aa. Then the solution for hexagon Ab must be 2, and for hexagon Ba must be 3 as shown in the next figure.
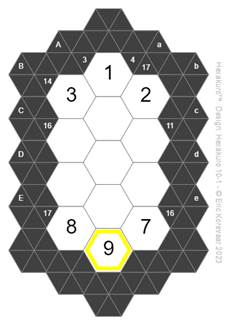
If we look at the bottom part of the puzzle, we can see a similar situation to the one just discussed for hexagon Ee. Diagonal “E” has a clue that two hexagons must add up to 17, and the only possibility is the set {8,9}. Diagonal “e” has a clue that two hexagons must add up to 16, and the only possibility with non-repeating numbers is the set {7,9}. The only overlap between these sets is the number 9, which must be the solution for hexagon Ee. It follows that the solution for hexagon Ed is 8 and for hexagon De is 7. This is shown in the next figure.
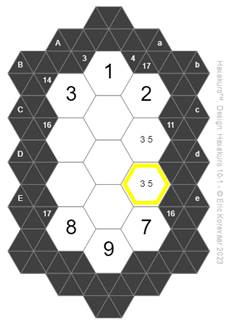
 Now
look at the column going from Ab to De. This column has four hexagons, so we
need four non-repeating digits that add up to the clue of 17. Two of these
hexagons are already solved with the numbers 2 and 7, which add up to 9.
Therefore, the other two hexagons (Bc and Cd) must have digits which add up to
17-9 = 8. The sets of two numbers adding to 8 are {1,7}, {2,6}, {3,5} and
{4,4}.
Now
look at the column going from Ab to De. This column has four hexagons, so we
need four non-repeating digits that add up to the clue of 17. Two of these
hexagons are already solved with the numbers 2 and 7, which add up to 9.
Therefore, the other two hexagons (Bc and Cd) must have digits which add up to
17-9 = 8. The sets of two numbers adding to 8 are {1,7}, {2,6}, {3,5} and
{4,4}.
We can eliminate {4,4} because repeating digits are not allowed.
We can eliminate {1,7} because we have already used a 7.
We can eliminate {2,6} because we have already used a 2.
That leaves us with {3,5}. It is useful to mark these in as “guesses” for the two hexagons. The app has a pull-down menu, or on a laptop you can use the control key before the guess number to mark it in. The puzzle with the guesses marked in is shown in the next figure.
 Since
the 3 is already used in diagonal “B” (at hexagon Ba), it follows that the
solution for hexagon Bc must be 5. Then the only remaining solution for
hexagon Cd is the number 3.
Since
the 3 is already used in diagonal “B” (at hexagon Ba), it follows that the
solution for hexagon Bc must be 5. Then the only remaining solution for
hexagon Cd is the number 3.
Now we can use the clue for diagonal “B” which has three numbers which must add up to 14. Since two of these numbers are 3+5=8, the remaining number must be 14-8 = 6. So the solution for hexagon Bb is 6, as shown in the next figure.
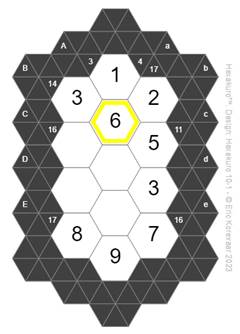 Our
example Hexakuro puzzle now has four remaining hexagons to solve for, and two
remaining unused clues. Consider diagonal “c” which has three numbers adding
up to 11. We have already solved for the 5 in hexagon Bc, so the other two
hexagons must add to 11-5 = 6. The sets of two numbers adding to 6 are {1,5},
{2,4} and {3,3}.
Our
example Hexakuro puzzle now has four remaining hexagons to solve for, and two
remaining unused clues. Consider diagonal “c” which has three numbers adding
up to 11. We have already solved for the 5 in hexagon Bc, so the other two
hexagons must add to 11-5 = 6. The sets of two numbers adding to 6 are {1,5},
{2,4} and {3,3}.
We can eliminate {3,3} because it has repeating numbers.
We can eliminate {1,5} because we have already used the 5.
That leaves us with {2,4} which have been marked in as guesses in the next figure.
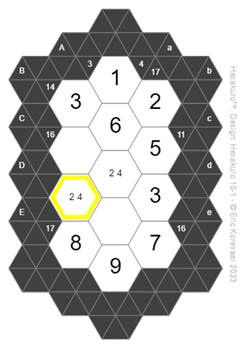 In
solving a Hexakuro puzzle, it will sometimes happen that two adjacent hexagons
have the same two possible guesses, as has happened here for hexagons Dc and Cc
with the guesses {2,4}. That means that another hexagon which is in the same
diagonal or column as those two cannot have one of those two numbers as its
solution. Specifically, the solution for hexagon Dd cannot be a 2 and cannot
be a 4.
In
solving a Hexakuro puzzle, it will sometimes happen that two adjacent hexagons
have the same two possible guesses, as has happened here for hexagons Dc and Cc
with the guesses {2,4}. That means that another hexagon which is in the same
diagonal or column as those two cannot have one of those two numbers as its
solution. Specifically, the solution for hexagon Dd cannot be a 2 and cannot
be a 4.
Now we can use our Sudoku skills to solve for hexagon Dd.
We can eliminate 1 because that is used in column Aa-Ee.
We can eliminate 2 because that is in either Dc or Cc.
We can eliminate 3 because that is used in diagonal “d”.
We can eliminate 4 because that is used in either Dc or Cc.
We can eliminate 6 because that is used in column Aa-Ee.
We can eliminate 7 because that is used in diagonal “D”.
We can eliminate 8 because that is used in diagonal “d”.
We can eliminate 9 because that is used in column Aa-Ee.
That leaves us with 5 as the solution for hexagon Dd.
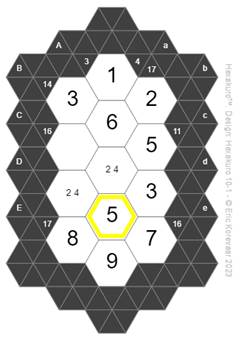 Looking
now at our last clue (diagonal “C”), we need three numbers which add up to 16,
one of which is a 3, and the other of which is in the set {2,4}. The only
possibilities are 16-3-2=11 or 16-3-4=9. Of course, 11 is not a single digit
number, so the solution to hexagon Cb must be 9 and for hexagon Cc must be 4.
Looking
now at our last clue (diagonal “C”), we need three numbers which add up to 16,
one of which is a 3, and the other of which is in the set {2,4}. The only
possibilities are 16-3-2=11 or 16-3-4=9. Of course, 11 is not a single digit
number, so the solution to hexagon Cb must be 9 and for hexagon Cc must be 4.
Finally that leaves 2 as the solution for hexagon Dc, and we are done!
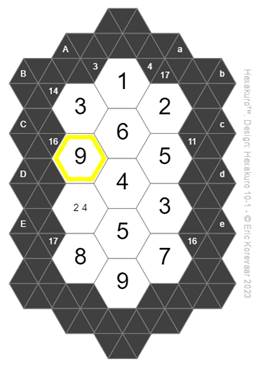
Features
There are some really nice features which you can use when solving a puzzle.
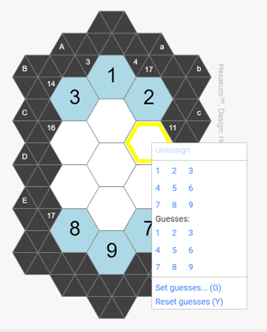 When you click on a hexagon you get a pull down menu.
The top grid of 9 numbers allows you to assign a solution to the hexagon (large number).
The bottom grid of 9 numbers allows you to input some guesses (small numbers).
These guesses toggle, so if you choose one of the numbers that is already in your guess box,
it will be removed.
When you click on a hexagon you get a pull down menu.
The top grid of 9 numbers allows you to assign a solution to the hexagon (large number).
The bottom grid of 9 numbers allows you to input some guesses (small numbers).
These guesses toggle, so if you choose one of the numbers that is already in your guess box,
it will be removed.
You can also enter solution numbers with your keyboard. To enter guesses use the control key and the number key.
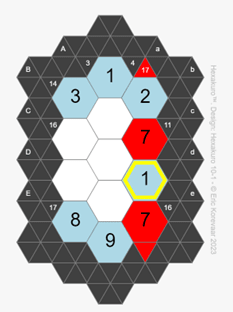 If you enter the same number twice in a column or diagonal,
the repeating number will be highlighted in red.
If you enter the same number twice in a column or diagonal,
the repeating number will be highlighted in red.
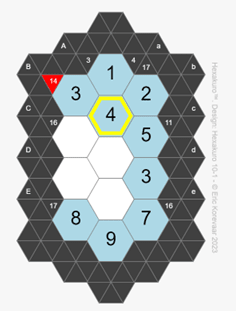 If you enter a number that causes a column or diagonal to sum to the wrong number,
the corresponding clue is highlighted.
In this case, the 14 clue is highlighted because 3+4+5 = 12 instead of 14.
If you enter a number that causes a column or diagonal to sum to the wrong number,
the corresponding clue is highlighted.
In this case, the 14 clue is highlighted because 3+4+5 = 12 instead of 14.
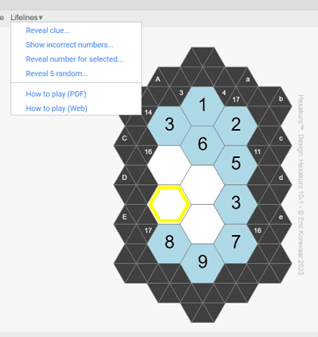 If you get stuck solving the puzzle, there are a number of Lifelines in a pull down menu you can take advantage of.
If you get stuck solving the puzzle, there are a number of Lifelines in a pull down menu you can take advantage of.
Show incorrect numbers (after confirmation) will show any hexagon solutions you have entered incorrectly.
Reveal number for selected hexagon will give the solution for the hexagon.
Reveal 5 random hexagons will give the the correct solution for five hexagons.
Reveal clue is a good way to make the puzzle a little easier if you are stuck, without actually looking at the solution to any particular hexagon. It works by allowing you to click on a triangle to reveal an additional clue as in the screenshot below.
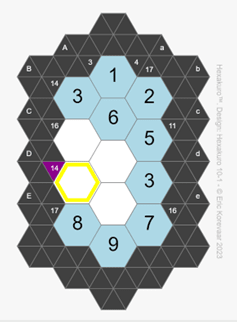 In this case, the extra clue for diagonal D has been provided, namely 14.
In this case, the extra clue for diagonal D has been provided, namely 14.
More
Check out this short YouTube video.
Go here to checkout some sample screenshots.
Check out screenshots and install from the Microsoft web store.
Launch the app.
File system integration
The app is (when installed) integrated with the host file system, i.e. you can use the 'Open with' feature to launch the app for a selected file.
Extensions that can be opened are:
- .hexakuro
- .hexakurot
Note that you have to install the app to enable file system integration.
See also
You might also be interested in these other apps or add-ons.
 Bjorn's Hexakuro Designer - a web app
Bjorn's Hexakuro Designer - a web app
Create fun and challenging math number puzzles
5-in-a-row is an abstract strategy board game, also known as Gomoku. The game is played with different markers on a board of 20x20. Once placed, markers are not moved or removed from the board.
 Bjorn's 5-in-a-row-3D - a game
Bjorn's 5-in-a-row-3D - a game
Play 3D-ish Gomoku-like games
 Bjorn's Memory Games - a web app
Bjorn's Memory Games - a web app
Play memory games
Pricing
This game can be used FREE of charge.
Support
Please report bugs here or reach out 2 me with questions @ support@backlund.org.
Follow me at Instagram @bjornsplayground and check out more videos at my YouTube channel.
You can view our privacy policy here.



